header
  • Home
  • Database
  • Info
  • References
  • News
  • Contact
  • Download
  • HZ calculator
  • p-p rate

    • Pre-Main Sequence models

    Tognelli, Prada Moroni, Degl'Innocenti

    2011, Astronomy & Astrophysics, 533, A109

    The database grid

    Pre-MS evolutionary tracks are available for:

    • 19 values of metallicity in the range Z= 0.0002 - 0.03
    • 3 values of the initial helium abundance (Y) for each Z
    • 3 values of the mixing-length parameter (α= 1.20, 1.68 and 1.90) for each chemical composition
    • 2 values of the initial deuterium abundance (XD= 2 · 10-5 and 4 · 10-5) for models with Z > 0.007
    • 43 stellar mass values in the range M= 0.2 - 7 Mo for each set of Z,Y, XD and α

    We computed also the corresponding pre-MS isochrones for ages in the range 1-100 Myr.

    The initial helium abundance of a model with metallicity Z follows from the linear relation:

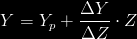
    where Yp is the primordial helium abundance (i.e. the result of the Big Bang nucleosynthesis) and Δ Y/Δ Z the ratio which provides the stellar nucleosynthesis enrichment.

    We provide pre-MS models adopting:

    • Yp=0.2485, Δ Y/Δ Z= 2 and 5
    • Yp=0.230, Δ Y/Δ Z= 2
    corresponding to the following values of [Fe/H]:

      Yp = 0.2485 Yp = 0.230
      ΔY/ΔZ=2 ΔY/ΔZ=5 ΔY/ΔZ=2
    Z [Fe/H] [Fe/H] [Fe/H]
    0.0002 -1.79 -1.79 -1.80
    0.0010 -1.09 -1.09 -1.10
    0.0020 -0.79 -0.79 -0.80
    0.0030 -0.61 -0.61 -0.62
    0.0040 -0.48 -0.48 -0.50
    0.0050 -0.39 -0.38 -0.40
    0.0060 -0.31 -0.29 -0.32
    0.0070 -0.24 -0.22 -0.25
    0.0080 -0.18 -0.16 -0.19
    0.0090 -0.12 -0.11 -0.13
    0.0100 -0.08 -0.06 -0.09
    0.0125 0.03 0.05 0.01
    0.0150 0.11 0.14 0.10
    0.0175 0.18 0.21 0.17
    0.0200 0.24 0.28 0.23
    0.0225 0.30 0.34 0.29
    0.0250 0.35 0.40 0.34
    0.0275 0.40 0.45 0.38
    0.0300 0.44 0.50 0.43

    The evolution code

    The structure and evolution of pre-MS models have been computed by means of the latest version of FRANEC (Tognelli, Prada Moroni, Degl'Innocenti 2011; Valle et al. 2009), a stellar evolution code based on the Henyey technique for solution of the equations of stellar structure and evolution.

    Convection

    The Schwarzschild criterion is adopted to identify the convectively unstable regions, where the mixing is assumed to be instantaneous. Concerning the treatment of convective transport in superadiabatic zones, typical of the outer stellar layers, the mixing length theory is followed (Bohm-Vitense 1958; Cox & Giuli 1968). In this framework the convective efficiency depends on the mixing length l= α Hp, where Hp is the pressure height scale and α is a free parameter to be calibrated.

    We calibrated the mixing length parameter with our Standard Solar Model obtaining α= 1.68.

    Diffusion

    The diffusion of helium and heavy elements is taken into account. Diffusion coefficients are computed following Thoul, Bahcall & Loeb (1994).

    Boundary conditions

    We use detailed model atmospheres as surface boundary conditions.
  • 3000 K < Teff < 10000 K: Brott & Hauschildt (2005)
  • 10000 K ≤ Teff < 50000 K: Castelli & Kurucz (2003)

    • Input physics

    Equation of state (EOS)

    We adopt the last version of the OPAL EOS (Rogers et al. 1996; Rogers & Nayfonov 2002). At low temperatures, the OPAL tables are extended by means of FreeEOS tables released in 2008 (Irwin 2004).

    Opacity

  • log T(K) > 4.5: OPAL radiative opacity (Iglesias & Rogers 1996)
  • log T(K) ≤ 4.5: radiative opacity by Ferguson et al. (2005)
    • We use the conductive opacity computed by Potekhin (1999), Shternin & Yakovlev (2006) The opacity have been computed for the recent solar mixture by Asplund et al. (2005).

    Nuclear Network

    The code take follows the burning of 26 elements. The reaction rates for the light elements (D,3He, Li, Be and B) and the hydrogen burning (p-p chain and CNO cycle) are taken from the NACRE compilation (Angulo et al. 1999), with the exception of the 14N(p,γ)15O which is from the LUNA collaboration (Imbriani et al. 2005). The initial abundances of 3He, Li, Be and B are from Geiss & Gloeckler (1998). We computed pre-MS models for two different initial abundances of D.
  • XD= 4 · 10-5
  • XD= 2 · 10-5

    • References

  • Angulo C., et al. 1999, Nucl. Phys. A, 656, 3
  • Asplund M., Grevesse N., & Sauval A.J. 2005, in ASP Conf. Series, Vol. 336, Cosmic abundances as records of stellar evolution and nucleosynthesis, ed. T. G. Barnes, III & F. N. Bash, 25
  • Bohm-Vitense E. 1958, Zeitschrift fur Astrophysik, 46, 108
  • Brott, I. & Hauschildt, P.H. 2005, in ESA Special Publication, Vol. 576, The three.Dimensional Universe with GAIA, ed. C. Turon, K.S. O'Flaherty, & M.A.C. Perryman, 565
  • Castelli F., & Kurucz R.L. 2003, in IAU Symp., Vol. 210, Modelling of Stellar Atmospheres, ed. N. Piskunov, W.W. Weiss, D.F. Gray, 20
  • Cox J.P., & Giuli R.T. 1968, Principles of stellar structures, New York, Gordon and Breach
  • D'Antona F., & Montalban J. 2003, A&A, 412, 213
  • Ferguson J.W., Alexander D.R., Allard F., et al. 2005, ApJ, 623, 585
  • Geiss J, & Gloeckler G. 1998, Space Science Reviews, 84, 239
  • Imbriani G., Costantini H., Formicola A., et al. 2005, European Physical Journal A, 25, 455
  • Iglesias C.A., & Rogers F.J. 1996, ApJ, 464, 943
  • Irwin A.W. 2004, FreeEOS Documentation
  • Potekhin A.Y. 1999, A&A, 351, 787
  • Rogers F.J., & Nayfonov A. 2002, ApJ, 576, 1064
  • Rogers F.J., Swenson F.J., & Iglesias C.A. 1996, ApJ, 456, 902
  • Shternin P.S., & Yakovlev D.G. 2006, Phys. Rev. D, 74, 043004
  • Thoul A.A., Bahcall J.N. & Loeb A. 1994, ApJ, 421, 828
  • Tognelli E., Prada Moroni P.G., & Degl'Innocenti S. 2011, A&A, 533, A109
  • Valle G., Marconi M., Degl'Innocenti S., &Prada Moroni P.G. 2009, A&A, 507, 1541
  • Ventura P., Zeppieri A., Mazzitelli I., &D'Antona F. 1998, A&A, 331, 1011

    •  

     

    The Pisa Stellar Evolution Data Base for low mass stars

    Dell'Omodarme, Valle, Degl'Innocenti, Prada Moroni

    2012, Astronomy & Astrophysics, 540, A26

    The low mass stars database contains two sets of tracks and isochrones.

    The first grid allow initial helium abundance Y and metallicity Z to vary independently. This set was computed for:

    • 19 values of metallicity Z in the range [0.0001 - 0.01]
    • 5 values of the initial helium abundance Y for each Z
    • 3 values of the mixing-length parameter (α= 1.70, 1.80 and 1.90) for each chemical composition
    • 2 values of alpha-enhancement of the Solar mixture ([&alpha/Fe] = 0.0, 0.3)
    • 17 stellar mass in the range [0.30, 1.10]

    The second grid is computed assuming a linear relation between Y and Z:

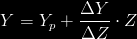
    where Yp = 0.2485 is the primordial helium abundance and Δ Y/Δ Z the ratio which provides the stellar nucleosynthesis enrichment.
    For each pair (Y, Z) stellar tracks was computed for:

    • 3 values of the mixing-length parameter (α= 1.70, 1.80 and 1.90) for each chemical composition
    • 2 values of alpha-enhancement of the Solar mixture ([&alpha/Fe] = 0.0, 0.3)
    • 17 stellar mass in the range [0.30, 1.10]

    For each set of parameters we provide:

    1. Output of the calculations beginning from the PMS and ending either at the helium flash (for M = [0.30, 0.50] MO) or at central hydrogen exhaustion (M = [0.55 - 1.10] MO).
    2. For each calculation reaching the helium flash in less than 15 Gyr: output of the calculations beginning from the Zero Age Horizontal Branch (ZAHB) model and ending at the onset of thermal pulses.
    3. ZAHB models, calculated in intervals of 0.01 MO. ZAHB were computed to span a sizeable range of the ZAHB effective temperature extension: from zero mass loss in RGB (ZAHB mass equal to the progenitor mass) to a mass equal to the one of the He core at RGB flash plus a small envelope of 0.026 MO.
    4. Isochrones computed in the typical GC age range, from 8 to 15 Gyr, with time steps of 0.5 Gyr.

    The evolution code

    In this section we list only the changes with respect to the FRANEC version used for computation of Pre-Main Sequence models described above.

    Solar mixture

    The Asplund et al. (2009) solar elements mixture were adopted in the calculations.
    The value of the mixing length parameter calibrated with our Standard Solar Model is α = 1.74.

    Nuclear Network

    For the reaction 12C(α,γ)16O we adopted the expression given by Hammer et al. (2005).

    References

    • Asplund, M., Grevesse, N., Sauval, A.J., & Scott, P. 2009, ARA&A, 47, 481
    • Hammer, J.W., Fey, M., Kunz, R. et al. 2005, Nuclear Physics A, 758, 363